A friend put me on to a course in information theory by the Santa Fe Institute. It’s a good course, I’m not a huge fan of the instructor. He tends to leave some things that I want to know about unsaid.
But he did raise an interesting point about probability and information. Since those are two things that I have some interest in, I took one of his points and will expand upon it in this post.
I have to summarize his lecture here, so bear with me, it’s important. To find the probability of a series of events (like a coin toss), you can examine all the possible states of the result and do some basic math. For example, in flipping a coin some number of times, the formula is
expected number of heads (or tails) = m / 2 +- 1/2 √m
Where m is the number of trials.
This is true, because we can count up all the possible states of the coin flips. Let’s say you flip a coin 100 or 1000 times. It’s possible to list all the possible states of the sequence of coin flips. I’ll do this for three coin flips because 100 would a little long.
HHH
HHT
HTH
HTT
THH
THT
TTH
TTT
There are 8 possible combinations of coin flips. In this case, the probability of getting one of these 8 states is 1/8. But what if we weren’t concerned about the order, just how many heads or tail. The number of cases where there are all heads is much small then when there are 1 head or 2 heads.
All heads = 1 out of 8
1 head = 3 out of 8
2 heads = 3 out of 8
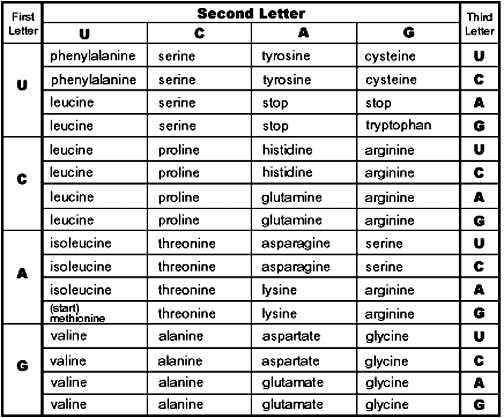
Something kind of similar happens in genetics. Not because we don’t care about the order of the nucleotides in DNA, but because sometimes a nucleotide doesn’t actually matter. First we’re going to need our codon chart.
Then we need a sequence of nucleotides. I’m going to try to get this as small as possible, so it’s easy to work with, but large enough to show the effects. I’m also going to ignore the start and stop codons.
UUU CCC AAA GGG CCC
When this is converted to a protein you get the following sequence.
phenylalanine(Phe) proline(Pro) lysine(Lys) glycine(Gly) proline(Pro)
That’s a very specific protein sequence.
Looking at that, there are 15 nucleotides. In this case, each nucleotide can be represented by 2 bits. This isn’t true in reality, which a huge issue for ID proponents, but again, for our case, it’s close enough.
The probability of that particular sequence appearing from a random collection of nucleotides is 1 in 415. That’s 1 in 1,073,741,824. Of course, no biologist thinks that a modern DNA sequence just popped into existence fully formed and ready to rock. That’s ID issue number 2.
But the nucleotides aren’t really the important part here is it? No, the important part is the resulting protein. And that’s interesting, because you can make some pretty massive changes to that DNA sequence and still get the exact same protein.
Phenylalanine can be coded by UUU or UUC.
Proline can be coded by CCC, CCA, CCU, or CCG.
Lysine can be coded by AAA or AAG.
Glycine can be coded by GGG, GGC, GGU, or GGA.
And I didn’t even use any of the proteins that are coded for by 6 combinations of nucleotides.
That changes our 1 in 1,073,741,824 probability to 256 in 1,073,741,824 or 1 in 4,194,304. Still pretty rare, but certainly not impossible. To put that in perspective, it’s only 10 times as improbable as getting a royal flush in 5-card stud.
But it gets even more interesting. The active site of a protein is where all the real work happens. That’s the part that does the chemical heavy lifting. The rest of the protein is just the scaffolding that puts the active amino acids in the correct place. Here’s an example
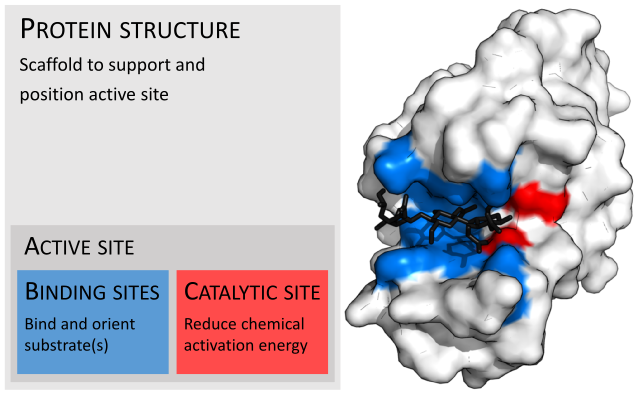
This particular molecule is the hen egg white lysozyme. Very often, the amino acids that in the white section can be any amino acid that fits a particular requirement. Maybe whatever amino acid in a particular spot must be hydrophobic, that is, water rejecting. Or maybe it needs to have sulfur or be acidic or basic. There are many properties that could be used to affect the shape of the final molecule.
How does this affect our probability? Using this as a simple example, let’s say that first four amino acids are the active site and that the last one can be anything as long as it is non-polar, like proline. Ten of the 20 amino acids are polar (Alanine, Valine, Leucine, Isoleucine, Proline, Tyrosine, Phenylalanine, Tryptophan, Methionine, and Cysteine). So probably any of those ten amino acids could be in that last spot.
In the codon chart, that’s 29 of the 64 possible combinations (if I did my counting correctly). So that changes our probability to about 1856 of 1,073,741,824 or 1 in 578,524. That’s almost exactly the same odds of getting a royal flush in 5-card stud. And we know that happens without divine intervention.
If you were to randomly mix the nucleotides, about 1 15-nucleotide string out of every half million random strings would be functionally equivalent to the first string I listed above.
Even if one was assume a random string of nucleotides (which is fundamentally mistaken), the odds of getting a functionally equivalent protein is significantly better than getting THAT string.
This has been done in the lab.
I need to add that what I’ve written here is based on a very simple DNA sequence. However, it doesn’t get more improbable when we move to longer and longer sequences and larger proteins. If anything, it become more probable.
In a discussion today, I learned that except for the active site itself and the point where the amino acid chain folds, the rest of the amino acids can be highly variable. Those fold points make up less than 5% of the protein. So you’ve got an active site that needs to be pretty specific (but doesn’t have to be exactly the same) and less than 5% of the rest of the protein that needs to be pretty specific.
But structural sequences are highly unlikely to suffer much from one or two random mutations. At worst it would change the denaturation temperature by a few fractions of a degree.
The examples I’ve presented and the comments from that discussion show that even many mutations to a gene can result in no noticeable change to the protein or protein function. Of course, some mutations do change the protein and now that protein can do something else or two different things. I’ve discussed that before.
There’s two takeaways here.
The first is that when someone says that a nucleotide sequence has to be that exact sequence, well, that’s just not true. There are a significant number of changes that can be made without affect any amino acid. And there are at least a few changes to the amino acid which do not affect the function of the protein.
For example, there are over 500 variations on hemoglobin. Five hundred variations on a protein that is absolutely critical to the survival of every individual. And that’s fine. Proteins (and the DNA sequences that code for them) can be highly variable.
Second is that people who try to calculate probabilities have to take into account these factors or they are wrong. One cannot accurately calculate a probability unless one considers all the factors. If a person can’t talk to you about the fact that protein construction (even from random materials) isn’t wholly random and talk about active sites vs. folding sites, vs structural amino acids, then that person isn’t worth listening to.