Painting Gabriel’s horn was the first in a series of posts on mathematical puzzles/paradoxes involving infinity. Next up is the Ross Urn Paradox. I learnt about this puzzle in Graham Oppy‘s excellent book Philosophical Perspectives on Infinity, where he attributed it to S. Ross’s 1988 statistics textbook A First Course in Probability. See also the Wikipedia article on the Ross-Littlewood Paradox, which involves a less specific version of the puzzle. Most of what I say here is in accord with Oppy’s treatment.
Oppy outlines three versions of the paradox, which I’ll detail below. First I’ll explain how each version works, and ask some questions. I’ll give my own answers to the questions after that, but make sure you try and work out your own answers before looking ahead – they really are fun puzzles, and you don’t have to be a mathematician to appreciate them.
In each version of the paradox, we start with a countably infinite collection of balls and an urn big enough to contain all the balls. A countably infinite sequence of steps are carried out. The first step takes place at 1 minute to midnight, the second step at 1/2 minute to midnight, the third at 1/4 minute to midnight, and so on. By the time midnight has ticked over, infinitely many steps will have been carried out. (Such an infinite sequence of tasks is known as a supertask.) The exact nature of the steps vary from version to version, but they all involve putting some balls into the urn.
Now of course, this is all in the realms of thought experiment, so don’t worry about the question of whether such a scenario is possible in our universe. (For what it’s worth, I don’t see why the standard conception of God as a maximally great being could not carry out any of the tasks described below – for related discussions, see my previous posts, Can God count to infinity? and Painting Gabriel’s horn.)
Ross Urn – Version 1.
Here we suppose the balls are labelled by the natural numbers 1,2,3,4,5,… And here are the steps:
Step 1.1. At one minute to midnight, Balls 1,2,3,…,10 are placed in the urn, and then Ball 1 is removed.
Step 1.2. At 1/2 minute to midnight, Balls 11,12,13,…,20 are placed in the urn, and then Ball 2 is removed.
Step 1.3. At 1/4 minute to midnight, Balls 21,22,23,…,30 are placed in the urn, and then Ball 3 is removed.
In general, at the nth step, the next 10 balls are placed in the urn, and the ball with the smallest label is removed. After the nth step, the urn contains Balls n+1, n+2, … , 10n, ie a total of 9n balls.
Question 1.1. At midnight, after all the operations have been carried out, how many balls are in the urn?
Question 1.2. If there are any balls in the urn at midnight, what labels are on the balls?
Have a think about your answers to these questions before moving on to the next version. I’ll give my own proposed solution to all the versions below. Make sure you have a good think about it before you look ahead!
Ross Urn – Version 2.
Here, again, we suppose the balls are labelled by the natural numbers 1,2,3,4,5,…, but we don’t use them all – we only use balls whose labels don’t end in a zero. Here are the steps:
Step 2.1. At one minute to midnight, Balls 1,2,3,…,9 are placed in the urn, and then a zero is painted to the right of the label on Ball 1, so that its label becomes 10.
Step 2.2. At 1/2 minute to midnight, Balls 11,12,13,…,19 are placed in the urn, and a zero is painted to the right of the label on Ball 2, so that its label becomes 20.
Step 2.3. At 1/4 minute to midnight, Balls 21,22,23,…,29 are placed in the urn, and then a zero is painted to the right of the label on Ball 1, so that its label becomes 30.
In general, at the nth step, the next 9 balls are placed in the urn, and the ball with the smallest label has a zero added to its label. Just like in the previous version, after the nth step, the urn contains a total of 9n balls, and these balls have the labels n+1, n+2, … , 10n.
Question 2.1. At midnight, after all the operations have been carried out, how many balls are in the urn?
Question 2.2. If there are any balls in the urn at midnight, what labels are on the balls?
It’s very tempting to suppose that the answers to Questions 2.1 and 2.2 should be the same as the answers to Questions 1.1 and 1.2 (fter all, if you looked in the urn at any stage between 11:59 and midnight, you’d see pretty much the same thing). But is that really the case? Don’t peek ahead! Have a good think about how you would answer these questions and then move in to the third version:
Ross Urn – Version 3.
Here we suppose the balls have no labels, but that inside the urn there are compartments labelled by the natural numbers 1,2,3,4,5,…, and that each compartment can fit exactly one ball. Here are the steps:
Step 3.1. At one minute to midnight, balls are placed in Compartments 1,2,3,…,9, and then the ball in Compartment 1 is picked up and moved to Compartment 10.
Step 3.2. At 1/2 minute to midnight, balls are placed in Compartments 11,12,13,…,19, and then the ball in Compartment 2 is picked up and moved to Compartment 20.
Step 3.3. At 1/4 minute to midnight, balls are placed in Compartments 21,22,23,…,29, and then the ball in Compartment 3 is picked up and moved to Compartment 30.
In general, at the nth step, balls are placed in the next 9 compartments, and the occupied compartment with the smallest label has its ball removed, and this ball is then placed into the compartment whose label is 1 more than the highest labelled occupied compartment. Just like in the previous two versions, after the nth step, the urn contains a total of 9n balls, and these balls are sitting in Compartments n+1, n+2, … , 10n.
Question 3.1. At midnight, after all the operations have been carried out, how many balls are in the urn?
Question 3.2. If there are any balls in the urn at midnight, what compartments are the balls in?
Here’s a little break so you don’t peek ahead by accident…
Here is how I think the questions should be answered…
Question 1.1. After Step n, there are 9n balls in the urn – those labelled n+1, … , 10n – so it seems sensible to suppose that there will be infinitely many balls in the urn at midnight, once all the steps are completed. But this is incorrect. Note that on Step 1, Ball 1 is removed from the urn. Ball 2 is removed on Step 2, and Ball 3 is removed on Step 3. In general, Ball n is removed in Step n. In other words, each and every ball is placed in the urn at some point, and then removed at a later time. Since each ball is removed from the urn, the urn must actually be empty at midnight.
Question 1.2. Well, there are no balls in the urn at midnight, so there is nothing to answer here!
Now this all seems quite strange. After all, there are 9n balls in the urn after Step n, and we all know that 9n tends toward infinity as n tends towards infinity. On the other hand, the answer of “empty” to Question 1.1 seems to make sense from the perspective of the set-theoretic limit. (I won’t go into details here, but will be happy to discuss it in the comments section if anyone wants me to.) Now let’s move on to the second scenario.
Question 2.1. If you looked inside the urn after Step n, you would see balls labelled n+1, … , 10n. Since these are the same labels as we saw in the first scenario after Step n, it seems sensible to suppose that the answers to Questions 2.1 and 2.2 will be the same as those to Questions 1.1 and 1.2. But, again, this is incorrect! To see this, simply consider the fact that once a ball is placed in the urn, it is never taken out again. On each step, 9 balls are added to the urn, and these remain in the urn the whole time (even though their labels change from step to step). So there must be infinitely many balls still in the urn at midnight, once all the steps are completed.
Question 2.2. To see how to answer this question, consider Ball 1. After Step 1, it has become Ball 10 (since a zero is painted at the end). During Step 2, nothing happens to this ball, and neither does anything happen on Steps 3, 4, 5, 6, 7, 8 or 9. However, on Step 2, Ball 2 becomes Ball 20. On Steps 3, 4 through 9, Balls 3, 4 through 9 become Balls 30, 40 through 90. By the start of Step 10, the smallest label on a ball is 10. So our original ball, which began as Ball 1 and is now Ball 10, becomes Ball 100 after Step 10. Similarly, after Step 100, our ball becomes Ball 1000. Later, it will become Ball 10000, then Ball 100000, and so on. By midnight, it will have had infinitely many zeros added to the end of its label – its label will be 100000000… – a one followed by an infinite list of zeros! The same can be said for any other ball. Remember that we only ever add to the urn balls whose labels do not end in zeros – but, by the end of all the steps, each of these balls will have an infinite sequence of zeros at the end. So the answer is that the labels on the balls are precisely those infinite strings a1a2a3a4a5… such that, for some m, ak= 0 for all k > m.
Note that this scenario makes sense of our intuition that the number of balls tends towards infinity as the number of steps tends towards infinity, but seems out of step with the set theoretic limit. Oh well, such is life!
Question 3.1. Here things get rather a lot more complicated. The short answer here is that I don’t think there is enough information in the scenario to determine a unique answer to the questions. It seems to depend on the internal structure of the urn and the compartments as I’ll now discuss.
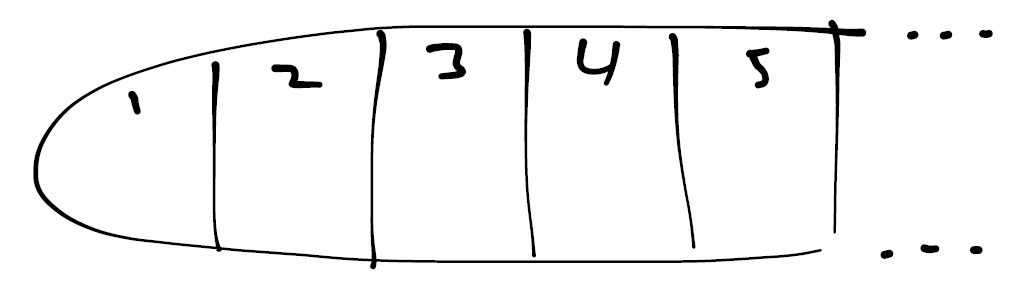
For example, suppose the urn looks like this, inside:
Please excuse my messy attempt at drawing on my iPad… Here the picture is meant to indicate that inside the urn (represented by the round outline) are the compartments (represented by the labelled squares). Now let’s consider what happens to the ball that is originally placed in Compartment 1. Let’s call the ball B for short. After Step 1, B is moved to Compartment 10. It stays there during Steps 2, 3 through 9, as the balls in Compartments 2, 3 through 9 are placed in Compartments 20, 30 through 90. Then, on Step 10, B is moved to Compartment 100. B is moved to Compartment 1000 on Step 100, then to Compartment 10000 on Step 1000, and so on. But where is B at midnight? It’s not in Compartment 1, since it was taken out of that compartment on Step 1. It’s not in Compartment 10, since it was taken out of that compartment on Step 10. Similarly, it’s not in Compartments 100, 1000, 10000, and so on. And it was never in any of the other compartments. So Ball B is not in any of the compartments. But where is it? Well, since we never took B out of the urn, it seems reasonable (but is it really?) to suppose that B is still in the urn, but just not in any of the compartments. The same line of reasoning leads us to the conclusion that none of the balls are in any of the compartments, but that they are all still probably in the urn.
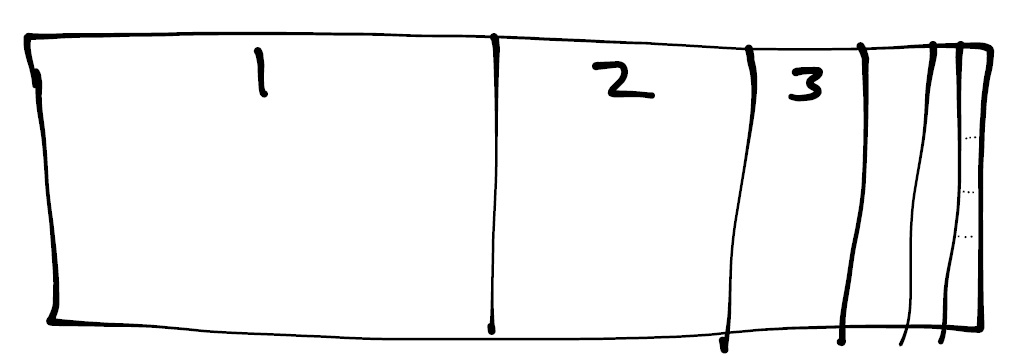
But what if the inside of the urn is completely made up of compartments as in the following picture:
Again, if we imagine what happens to some fixed ball, we see that by midnight, it is not in any of the compartments. Since the urn here is completely comprised of compartments, it seems reasonable to suppose that the balls are all outside the urn. This may seem counterintuitive, since at no step did we ever take a ball out of the urn. However, imagine the ball that starts in Compartment 1. On Step 1, it is moved to Compartment 10. It is moved to Compartment 100 on Step 10, then to Compartment 1000 on Step 100, and so on. By midnight, once all the steps are completed, the ball has made infinitely many such movements – it has traveled past every single compartment, so it does seem to make some kind of sense to accept that it is now out of the urn.
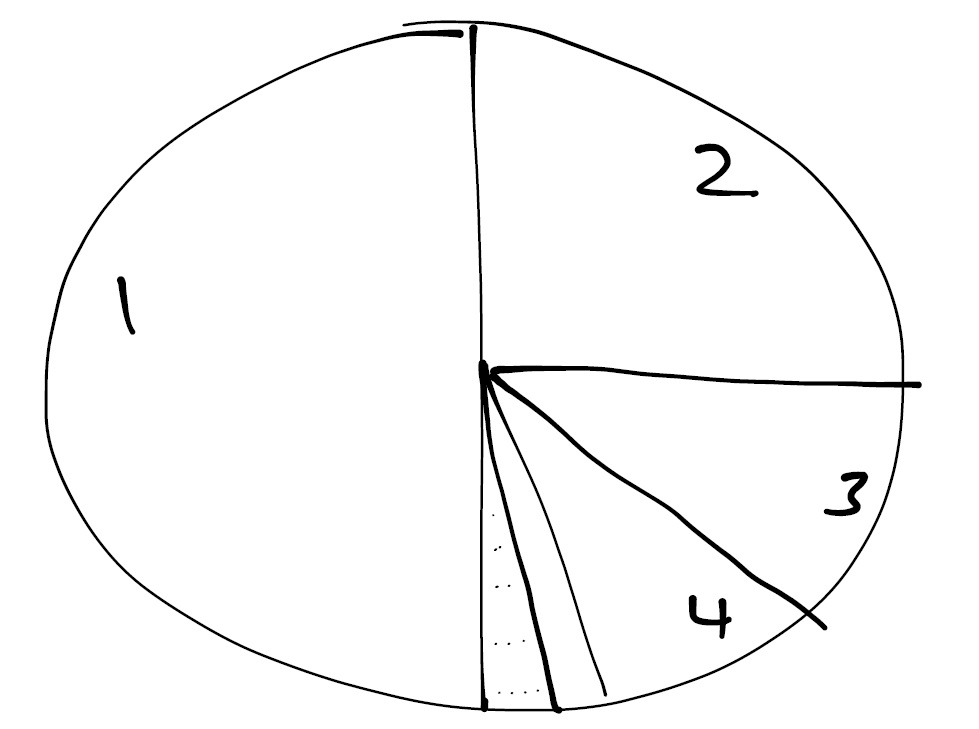
Now I know that last bit might sound even stranger – if the ball has traveled past infinitely many compartments, how could it have arrived somewhere? In other words, if compartments stretch out infinitely far to the right (as the picture indicates), how could it be that there is something even further to the right of them? Well, what if instead the urn looks more like this:
Even though this version of the urn is made up entirely of infinitely many compartments, each compartment is half the size of the previous one. So, if the first compartment is one metre wide, then the whole urn is a total of 1 + 1/2 + 1/4 + 1/8 + … = 2 metres wide. (We would also have to assume that the width of the walls between compartments gets smaller and smaller as we look from left to right.) Here we have another problem. Again consider the ball that starts in Compartment 1. Let’s call this Ball B again. Suppose B is 1 millimetre wide. After Step 1, B is placed in Compartment 10. Now, Compartment 10 is half the size of Compartment 9, which is half the size of Compartment 8, and so on. We see in fact that Compartment 10 is actually 1/29 = 1/512 the size of Compartment 1. In other words, Compartment 10 is approximately 1.95 millimetres wide. So B will indeed fit in Compartment 10. But it won’t fit in Compartment 11, which is approximately 0.98 millimetres wide (half the width of Compartment 10). If it doesn’t fit in Compartment 11, it has no hope of fitting in Compartment 100, which is where the ball is headed on Step 10! But it also has to get squashed into Compartment 1000, then 10000, and so on. No matter how small the ball is, at some point on its travels, it will find itself trying to squeeze into a compartment that just doesn’t have enough room for it. It seems the only hope of keeping the story consistent is to suppose that at each step, when a ball is moved from one compartment to a later compartment, the ball is shrunk on its way to its destination (or cut into two pieces, one of which is small enough to fit into the tiny compartment it is bound for). But what will be the state of Ball B at midnight? Perhaps the more important question has become “How big will the ball be at midnight?”. And the answer seems to be that the ball will be nonexistent – or at the most, it will be a single point. Indeed, after the first step, the ball is smaller than the width of Compartment 10. After Step 10, the ball is smaller than the width of Compartment 100, and so on. By midnight, the ball is smaller than the width of each of Compartments 10, 100, 1000, 10000, and so on. And the only (non-negative) number that is smaller than each of these widths (which tend monotonically towards zero) is zero! And, if we suppose that a ball of zero width is no ball at all, then I guess at midnight, there are no balls in the urn at all, much in accord with the first scenario!
Here’s another way the compartments could be arranged inside the urn:
I suppose the possibilities are endless… But it seems clear enough that there could be different answers to the Questions 3.1 and 3.2 depending on the internal structure of the urn.
Some people think that supertasks such as those described above are logically impossible – that they cannot be performed in any logically possible world (where we might relax ideas such as matter being composed of elementary particles and so only finitely divisible). Perhaps some supertasks are logically possible, and some are not. Some people think that, if such supertasks are logically impossible, then the very notion of an actual infinity is absurd. But I don’t see why this should be the case. Again, perhaps some kinds of actual infinities are possible while others are not. But, as I’ve argued elsewhere, I think the standard theistic conception of God as (among other things) essentially unbounded when it comes to things such as speaking, thinking, moving, etc, is a being that ought to be able to perform supertasks such as counting to infinity, or painting an infinite shape – and I don’t see why any of the Ross Urn scenarios should pose a greater challenge. If a theist wishes to argue against the possibility of actual infinities (perhaps in order to argue that the universe/multiverse could not be past eternal), then they had better modify their conception of God!
