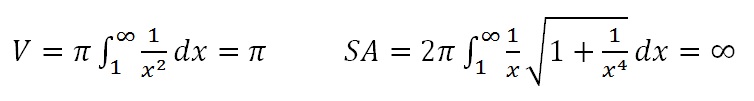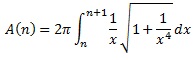I thought I’d do a couple of posts about some interesting mathematical paradoxes. These don’t strictly have anything to do with religion or atheism (except that certain apologists seem to think some puzzling mathematical phenomenon lend support to the existence of God).
First up is a shape with finite volume but infinite surface area. Check it out!

This shape is known as Gabriel’s Horn, and the picture is from the informative Wikipedia article. If you’re curious, the horn is obtained by rotating the curve y = 1/x, from x = 1 to ∞ around the x-axis. The main thing you need to know, though, is that it is essentially a trumpet/horn kind of thing that keeps going on and on for ever and ever, getting thinner and thinner, but never closing off. This video does a fine job of explaining how to calculate the volume and surface area of the horn. Basically, it comes down to evaluating the integrals:
(The symbol “π” is the Greek letter “pi”, their equivalent of our letter “p”. It stands for the number that is approximately 3.14159 – a very important number in mathematics – if you measure around a circle, and across it, then divide the big number by the small one, you’ll get π every time, no matter how big or small the circle is.)
So the volume of Gabriel’s horn is finite (π units cubed) but the surface area is infinite. This in itself doesn’t seem paradoxical, until you start to think about practical matters.
Imagine you wanted to paint the interior of the horn. How much paint would you need? Well, the surface area is infinite, so you’d need an infinite supply of paint, right? But, on the other hand, the volume of the horn is finite. You could tip the horn on its side and completely fill it up with approximately 3.14159 litres of paint. And then you’d just have to pour out the paint, and the paint that had stuck to the sides would leave you with a freshly painted interior! But how can that be? Didn’t we just decide you need an infinite supply of paint to coat the interior? Yet now it seems you can paint the interior with not much more than 3 litres of paint! What’s going on??
Now, I’ve looked around the internet and seen quite a bit of discussion of this paradox, but nothing that I would call a satisfactory resolution to it, and that’s why I felt like writing this post. (That and because it’s fresh in my mind after teaching my undergrad calculus students about the paradox the other day.)
Now, what exactly is it that makes this a paradox? One line of reasoning leads us to believe that the interior of the horn cannot be painted with a finite amount of paint, but another line of reasoning leads us to believe it can. Essentially, it feels as if we are are forced to affirm the following two contradictory statements:
Statement 1. The interior of the horn cannot be painted with a finite amount of paint because its surface area is infinite.
Statement 2. The interior of the horn can be painted with a finite amount of paint because its volume is finite (meaning you could fill it up with paint and then tip it out).
Before I give my own thoughts on the paradox, let me outline a few attempted resolutions I’ve encountered online.
Explanation 1. You can’t fill the horn up with paint because it would take forever. No matter how long you were pouring paint into the horn, there would still be parts of the horn that weren’t yet filled. Likewise, it would take forever to tip the paint out. So Statement 2 is false.
Explanation 2. Paint is a physical thing – it is made up of atoms. At some point, the horn gets so thin that even the tiniest atom would get stuck in it. In other words, you couldn’t fill the horn up with paint. And this means you can’t paint the horn by this trick. So Statement 2 is false.
These two explanations say that there is something physically impossible about the situation. You can’t paint the horn or fill it up with paint because of some property either of paint (it is not infinitely divisible) or of time (we can’t wait forever for the horn to get filled up). More such complaints could be made; for example, one could claim that it would be impossible to make the horn in the first place, or that it would be impossible to tip it over.
On the one hand, I agree that these kinds of explanations get us off the hook in the sense that we couldn’t make such an object in our universe, let alone paint it or fill it up with paint. But this is not really what the paradox is getting at. The paradox is really about logical possibilities, not possibilities subject to the physical constraints we are accustomed to. For example, Statement 1 isn’t really saying “you couldn’t actually coat the interior of the horn with paint because its surface area is infinite” – it’s saying the much stronger “there could not be a state of affairs in which the interior of the horn has a coat of paint all over it, using a finite volume of paint, because its surface area is infinite”. The only kind of explanation I’ve heard that takes this into account is the following:
Explanation 3. We’re talking about perfect mathematical paint here, and everyone knows mathematical paint is infinitely thin. So you can indeed paint the horn, even though it has infinite surface area (one way to do this being to fill it up with π litres of paint and then tip the excess paint out, leaving a coating of zero thickness). So Statement 1 is false.
While I think this is getting closer to the right idea, there still seems to be a certain sense in which it is cheating. Even if we suppose that the horn could exist (in some logically possible world), and that it could be filled with paint, we should probably still think of paint as something that has nonzero thickness. It seems question begging to assume that in any version of reality in which Gabriel’s Horn could exist, paint can be spread infinitely thin. It seems that to adequately resolve the paradox, we should concede that to say “a surface has a coat of paint on it” is to say “at each point on the surface, there is a finite (but nonzero) thickness of paint on it”. The question we need to answer becomes:
Is there a state of affairs in some logically possible world in which Gabriel’s Horn has a coat of paint all over it, such that (1) at each point on the surface of the shape, there is a finite but nonzero thickness of paint, and (2) the total volume of paint is finite?
Recall that we are trying to resolve the apparent conflict between Statements 1 and 2 above. To do this, we need to show why (at least) one of them should not be believed. It’s not enough to say “they can’t both be true because they contradict each other, so one of them must be false”. It could actually be that correct reasoning from some other assumptions leads to the truth of both statements – this would then imply that one or more of our other assumptions was false (perhaps the idea that infinite shapes make sense at all). Rather, we need to show that there is something wrong with the reasoning that led us to think (at least) one of the statements might be true. And I think the dubious reasoning occurred when we tried to convince ourselves that Statement 1 is true – in particular, I don’t think that having infinite surface area automatically prevents a shape from being painted.
Now, of course in a world in which no infinite task can be carried out, or in which paint is not infinitely divisible (because, for example, it is made up of atoms), Statement 2 is obviously false, so the paradox poses us no problems at all. So let’s suppose we’re not in such a world. And a world in which Statement 2 is false is, again, obviously no problem to us. So let’s suppose Statement 2 is true in some possible world W, with the goal being to show that Statement 1 must be false in W.
In particular, we’ll suppose that there is a state of affairs in W in which Gabriel’s Horn is completely full of paint. In everything that follows, we’ll be restricting our attention to this particular world, W. (And, as mentioned above, we won’t worry ourselves with the mechanics of how it was filled, etc. If any of these tasks could not be performed in W, the paradox would pose us no problems.) Well, what are some of the properties of this paint in W? The most important property for our purposes is that it can be spread arbitrarily thin, as I’ll explain next.
If you take a look at the picture of the horn above, you’ll see that it has been (conceptually) divided into segments by the red circles on its exterior. Let’s denote these segments by S(1), S(2), S(3), and so on, and assume the segments are 1 unit wide. Since the horn is the result of rotating the graph y = 1/x about the x-axis, the nth segment, S(n), has a maximum thickness of 2/n units (at its left hand end) and a minimum thickness of 2/(n+1) units (at its right hand end). Since we have assumed it is possible for the horn to be full of paint, it follows that it is possible for the nth segment of the horn to be full of paint; in particular, it is possible for a nonzero quantity of paint to occupy a space of height at most 2/n. Since this is true for every value of n, it follows that the paint can be spread to a thickness of 2/n for any value of n. In particular, since 2/n can be made arbitrarily small by choosing n large enough, it follows that the paint can be spread arbitrarily thinly. Note that this last statement is not saying that the paint can be spread “infinitely thinly” (ie, to zero thickness). Rather, it is saying that for any given number t > 0, the paint can be spread to a thickness of t or less. (Indeed, just choose n to be an integer that is greater than 2/t. Then the paint in the nth segment of the filled up horn will have a thickness of at most 2/n, which is less than t.)
For each n, let’s write A(n) for the surface area of the segment S(n). Although it is not important, these surface areas are given by the formula:
And now we consider the state of affairs in which S(1) has a total of 1/2 litres of paint spread across it, S(2) has 1/4 litres of paint spread across it, S(3) has 1/8 litres of paint, and so on. Nowhere in this description are we saying that the paint is spread “infinitely thinly”. Indeed, segment S(n) is meant to have 1/2n litres of paint spread across it and, to achieve this, the thickness of paint will be 1/(2n×A(n)), which is certainly finite. Furthermoreover, the total amount of paint used is equal to:
![]()
litres. So we actually only needed 1 litre of paint – not the whole π = 3.14159 litres!
To summarize, the truth of Statement 2 (in some possible world) entails the falsity of Statement 1 (in the same world), so there is no logically possible world in which both statements are true. There is really no paradox after all.
But I think these considerations raise another interesting question. Is there a logically possible world in which someone could actually make the horn, fill it with paint, etc? Well I don’t see why the standard conception of God as a maximally great being couldn’t do it (as long as this conception of God is deemed to make sense). I argued in a previous post, Can God count to infinity?, that such a God could count to infinity by speeding up his counting as he went. And here I think the same kind of thing should be possible. Suppose God is standing in front of Gabriel’s Horn with a 1 litre bucket of paint in his hand. At midnight, he spends 1/2 an hour spreading 1/2 a litre of paint over the first segment of the horn. Then he spends the next 1/4 hour spreading 1/4 litre of paint over the second segment of the horn, then 1/8 hour spreading 1/8 litre over the third segment, and so on. By 1 am, he’ll have finished painting the horn – not a single part will have been left out! An actual infinite, achieved by successive addition!