William Lane Craig and James Sinclair’s chapter on the Kalam Cosmological Argument in the Blackwell Companion to Natural Theology contains a couple of arguments against the possibility of an infinite past. Here’s one of them:
P1. An actual infinite cannot exist.
P2. An infinite temporal regress of events is an actual infinite.
P3. Therefore, an infinite temporal regress of events cannot exist.
I’ve already talked about this argument in a few places:
And a few more posts will be devoted to this topic. But here I’ll consider another angle.
In defending their argument, Craig and Sinclair consider several possible refutations to the premise P1. One of these is that the existence of infinitely many numbers (and other kinds of mathematical objects) might directly contradict P1.
As Craig and Sinclair observe, this raises a very interesting question. In what sense can it be said that mathematical objects like numbers exist? Do they exist as material objects, perhaps only as configurations of neurons in the brains of humans? Do they have some kind of disembodied existence in a platonic mathematical realm? Or is there really no meaningful sense in which numbers can be said to exist? Is there some other explanation?
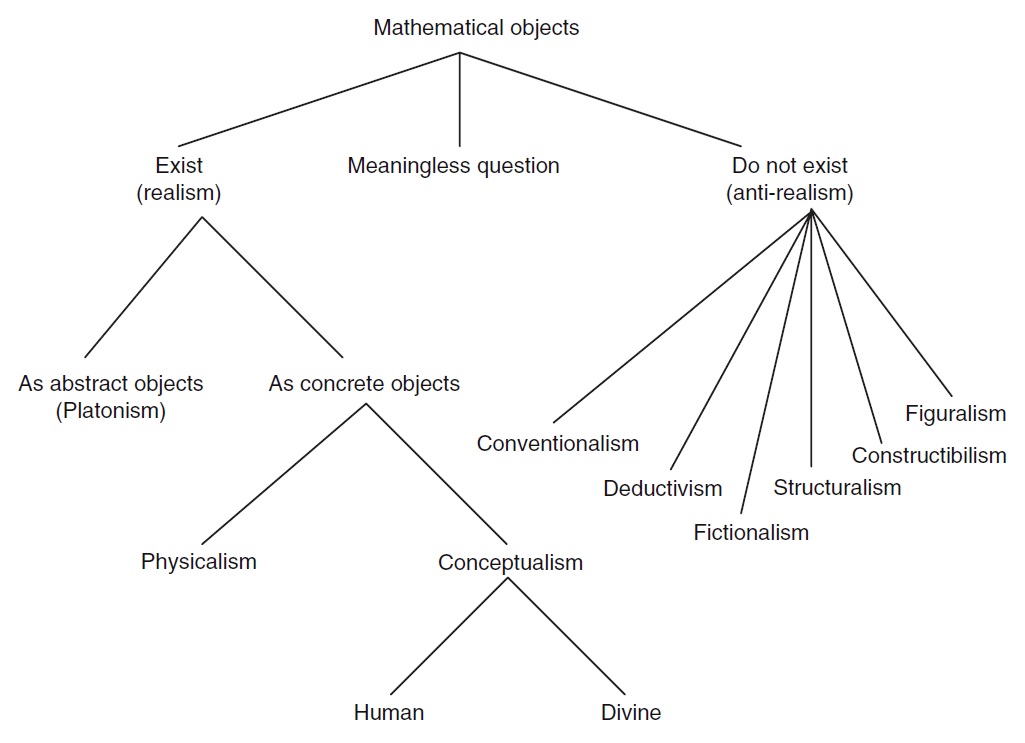
As a mathematician, I find these questions fascinating, though I certainly don’t claim to know the answers. I’ve talked about these ideas with several of my colleagues over the years, and discovered that there are a range of views, and also a range of associated confidence levels. The following diagram from the chapter illustrates several different kinds of theories of mathematical ontology (ie, theories about the existence of mathematical objects):
There are certainly a lot of views! To me, none of them seem likely to be provable – at least not in a strict sense – and I think the range of views held by professional mathematicians and philosophers counts as evidence that there does not currently exist a definitive proof one way or another. With that said, though, I do have doubts about a few of them. Some people have argued that we shouldn’t accept anything like a platonist view, for example, since there is no evidence that platonic objects exist. But, according to a recent survey, 39.3% of professional philosophers are platonists (with 37.7% nominalists and 23.0% choosing some other option). Most arguments I’ve heard seem to suggest that agnosticism is a reasonable position to take on the matter.
Now, returning to Craig and Sinclair’s argument, we see that consideration of mathematical objects only proves to be a decisive refutation to P1 given certain realist views of mathematical ontology. Here is how Craig and Sinclair put it:
“The Realist, then, if he is to maintain that mathematical objects furnish a decisive counterexample to the denial of the existence of the actual infinite, must provide some overriding argument for the reality of mathematical objects, as well as rebutting defeaters of all the alternatives consistent with classical mathematics – a task whose prospects for success are dim, indeed. It is therefore open to the [apologist] to hold that while the actual infinite is a fruitful and consistent concept within the postulated universe of discourse, it cannot be transposed into the real world.”
[As an aside, it seems that Craig and Sinclair are urging an insider of the Mathematical Realist camp to rationally assess his beliefs, and subject them to the same level of scrutiny he might demand of others. Is this an Outsider Test for Mathematical Ontology?]
The astute reader will have noticed that Craig and Sinclair are attempting to shift their burden of proof here. They are making the argument. And they must offer support for their premises. If they are aware that the existence of mathematical objects could cast doubt on one of their key premises, then they must adequately deal with this possibility. It is not enough to simply say that they think it would be difficult for an opponent to conclusively refute the premise.
It is true that to conclusively refute P1 by considerations of mathematical objects, one must demonstrate the validity of a theory of mathematical ontology that involves the actual existence of mathematical objects.
But, on the other hand, to conclusively prove P1, Craig and Sinclair (or someone else) must demonstrate the validity of a theory of mathematical ontology that involves the actual non-existence of mathematical objects – which I think Craig and Sinclair would probably agree is also “a task whose prospects for success are dim, indeed”. If they do not successfully do this, we are left wondering if perhaps mathematical objects do provide a counterexample to P1. But how might one prove such an assertion? Proving the non-existence of mathematical objects seems akin to proving the non-existence of god(s)!
In conclusion, I don’t know which theory of mathematical ontology is the correct one, and I don’t think Craig and Sinclair do either. If some form of platonism is correct (as is believed by nearly 40% of professional philosophers), mathematical objects would indeed provide a decisive counterexample to P1. And, unless this possibility can be ruled out, we have no compulsion to accept the premise – or the conclusion of any argument that relies on it.