Paradoxes are concepts or phenomena that seem self-contradictory, but may not be, or they may be thought experiments that appear to predict mutually exclusive outcomes. They are psychologically interesting because often they represent questions our minds are able to ask, but not answer, or not intuitively answer. I expect most readers of this space have heard of most of these, but you may not know that many are considered resolved or how they may be resolved. So here are answers to ten of them stated briefly, cliff-notes style. I do not claim these are authoritative, exclusive, or original replies (I will cite sources if I know them).
MC Escher’s energy-efficient stairmaster prototype.
Also I am picking ten from a YouTuber’s list because you can watch this video of Matthew Santoro to see the explanation of what the paradox is if you do not already know. I will not provide much in the way of descriptions. Matthew is an engaging guy and his videos are well-made and lively.
1. The Ship of Theseus.
More akin to an illusion, this paradox is not resolvable because it highlights the limitations of a psychological intuition (identity is an essence). Essentialist intuitions about identity are part of our evolved psychology because they are useful, even if untrue in a strict sense. Even if a ship (or mind) changes slowly over time, there’s still only ever one of them and the characteristics it had in the past strongly correlate with those that it has now and probably in the future, as if there were an essence. The paradox breaks this intuition by constructing a duplicate from the old parts. So one answer is that the concept of identity fails because it includes assumptions that are not guaranteed to be true.
Another possible answer is that the process is a kind of reproduction and the second copy is an offspring. Consider how a cell reproduces. It has to take in building materials from the environment: proteins, ions. It uses those to make more cytoplasm, membrane, organelles etc.., but again, using new “pieces” in addition to the old. Growth and reproduction is constantly about adding new bits and losing old ones. In what sense is a cell we’re looking at right now the “same” cell a week later? It isn’t. It has no stable identity. And maybe, neither do we.
2. The Omnipotence paradox. Could God create a rock so large that he could not lift it?
Omnipotence is just an idea, and not a plausible one. This paradox is a remnant of magical-theological thinking. If you’re going to start with a premise “a thing is supernatural and unbeholden to any physical rules or laws” nothing you say next on the matter is meaningful. This “paradox” is really just an illustration of why the idea makes no sense. Unlike some paradoxes (e.g. Zeno’s), there is no physical evidence as a premise nor any reason we should entertain the idea as true.
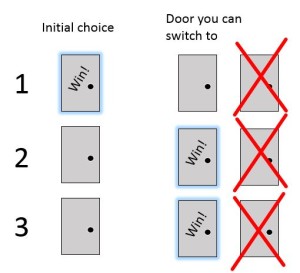
3. The Monty Hall paradox.
Why do you win 2/3 of the time after switching choice of doors? Why isn’t it 50/50? There are lots of long explanations like this one. I will make it simpler. This image shows the three doors which you might pick at random. To the right of each choice we see what the switched-to door has to be in each of these cases because Monty always removes a wrong choice. In two of the three conditions, Monty will always leave the correct choice. Only in one possible condition, that you guessed correctly off the bat, are you wrong to switch.
4. The unexpected hanging paradox.
This is a cheat-y paradox. It relies on the psychological belief of the convict, which the judge could not possibly know in advance, making his prediction sheer magic, or arbitrary premise of the paradox. If the convict has heard of the paradox before the sentencing or simply knows the judge has a knack for game-playing, then the paradox falls apart because the convict would know the judge is game-playing and apt to ignore logical evaluation or use it as a deception device. If the convict can’t reason about the psychology of the judge, then it is equally wrong for the judge to be reasoning (exploiting) the psychology of the convict. If they can both consider the psychology of the other, the paradox fails.
5. The Grandfather paradox.
The answer is much the same as number 2. We often wrongly conceptualize the past or future as if they were places instead of times. Most likely, the past is not something that exists. You can’t put it in a coherent sentence about the movement or location of objects including people. Like the omnipotence paradox, once you entertain the basic premise, you get all sorts of nonsense and violations of basic physical laws like relativity, the speed of light, conservation of energy et cetera. If you accept as a premise “thing that inexplicably breaks many basic laws of physics” you’ve essentially made a premise of magic, and whatever you say next is not meaningful.
6. The Barber’s paradox (Russell’s paradox).
Bertrand Russell himself pointed out that this form of this type of paradox is not valid. The premises are false and there is no phenomena in nature that indicates it could be otherwise. Either the barber is unshaved (disqualifying a premise) or else he does it himself (disqualifying a premise). How the hypothetical barber parses the rule does not matter; the premises are false no matter the action taken by the actor. There are more exacting forms of this paradox, but Russell’s reply is similar in kind, that it requires a nonsensical premise that can be readily shown to be nonsensical.
7. Fletcher’s paradox (aka Zeno’s Arrow paradox).
The key flawed assumption here is that there is such a thing as an “instant” in which motion is not occurring because time is not moving forward. But “instant” is just a concept and it doesn’t exist in reality the way the paradox uses it as a “frozen time”. Perhaps it takes the arrow 5 seconds to travel 100 yards. We would not consider 5 seconds an “instant”. How about 1 second? That won’t work, because at the start of the second it would be at one place, but at the end it would be 20 yards away. At 1/20th of a second it’s still moved a yard. At what time length would it be so small that zero distance was traveled? There is no such time length. It will always be moving, right up until we’re talking about durations so short that Heisenberg’s uncertainty principle prevents us from measuring the object’s speed and location accurately. If you think “instant” is just a time index instead of a unit of time, you remove its dimensions and render it irrelevant to considerations of motion in just the same way that between any two points on a line there are an infinite number of (indexical) points in between because the points are dimensionless. But objects in reality aren’t dimensionless (or motionless). This is similar to the dichotomy paradox, another of Zeno’s paradoxes. The resolution is the same, except more about space than time: there is a minimum unit of distance that can’t be split.
8. Liar paradox (Epimenides paradox). “This statement is false”.
Among the various replies from philosophers, I like this one from Arthor Prior (he credits CS Pierce and John Buridan). The idea is that all asserted statements implicitly and intrinsically positive declarations. That is, one does not have to say “This statement is true and it is presently noon” when they wish to say “It is presently noon.” The two are semantically identical. Therefore these two
This statement is false
This statement is true and this statement is false
are equivalent. Since the latter is invalid, the entire expression is false without being self-contradictory.
9. Sorites paradox (paradox of the heap).
Similar to the Ship of Theseus. “Heap” has no precise definition and the definition it does have will be subjective, but real. So at some point people will refuse to call something a heap as it gets further from their idea of what a heap is. That idea is analog and continuous (one pile can be more heap-like than another) so the boundary is fuzzy enough that removing one element is never decisive. That said, if you tested this you would probably find a small range of elements that people preferentially found to be determinate of “heap-ness”.
10. Raven paradox (Hempel’s paradox).
A. All ravens are black
B. Everything that is not black is not a raven.
C. This apple is green and not a raven.
B is a logical equivalent version of A. C seems to be evidence for A.
C actually is evidence for A. In fact, this has been evaluated using Bayesian analysis and found to be true. The reason it seems wrong to us is that the degree or power of the evidence is miniscule. So low it doesn’t register in our minds as evidence. But that’s not because it isn’t evidence, it’s because we intuitively cordon off types of evidence by their relative significance or utility. Not merely by the binary categorical status as evidence or not.
Let’s simplify the scenario so that you can see why this is true. Imagine that there is a universe with just 10 objects in it. Half are black and half are green. One is a black raven and there’s at least one more raven of unknown coloration. You’ve not yet seen any of the other nine objects, then you see a green apple. Does this affect the likelihood that “all ravens are black” is true? Yes, because it proves 20% of all green objects in the universe are not ravens. Only four other objects can disprove the rule. Each one of those you check reduces the statistical possibility the statement will turn out to be wrong. After you’ve seen four of the green objects, the last one you have not seen will prove to 100% certainty the statement is true… even though none of these objects are ravens.
Hempel pointed out that what really makes this a paradox is that we have prior knowledge which informs about the relevance of kinds of evidence, as opposed to blindly using abstract logical widgets. The paradox is about ravens and apples, which invokes everything you know about those.
True paradox?
There you are, now you may go and spoil the fun for people. Some will argue paradoxes with a pretty definitive resolution such as the raven or Zeno’s are not “true” paradoxes because they are resolved. This is not so because a paradox is really defined as something that seems impossibly self-contradictory but is not. That is, like a cognitive illusion. When we understand why an optical illusion exists, it does not cease to be an optical illusion. I might argue some of these are not “true” paradoxes on the basis of their arbitrary contrivance premises. Namely, omnipotence and the unexpected hanging. But most of these continue to violate our intuition, even if we understand why.