Happy Pi Day, everybody!
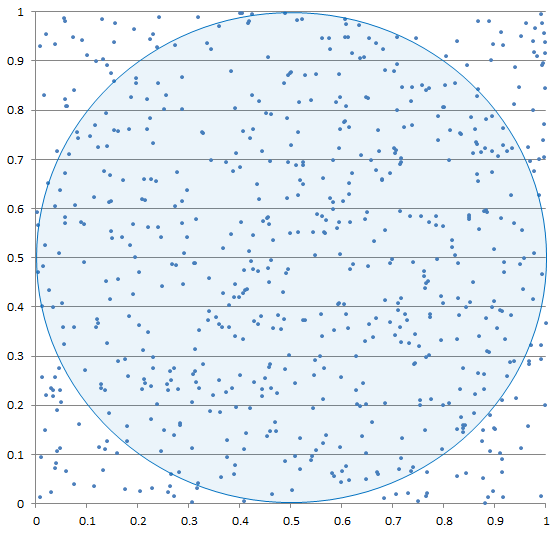
There are literally dozens of ways to compute π, ranging from geometrical approximations to series expansions to modern computational algorithms. I’m not going to go into all that here and now. Instead, for a quick and easy and above all probabilistic way to explain how to derive π to your kids, I’m going to suggest the analogy of a dartboard. If the dots on this chart were scattered uniformly at random throughout the square, what would be the probability that one of them falls inside the circle?
The area of the inscribed circle is π*r*r and the area of the square itself is 2r*2r, dividing the former by the latter we see that the ratio of the area of the circle to that of the square is π/4. Accordingly, the value of π can be approximated by throwing enough random dots at the square, computing how often they fall inside the circle, and multiplying by four. The law of large numbers should ensure that the computed average will converge upon the expected value in the long run, like so:
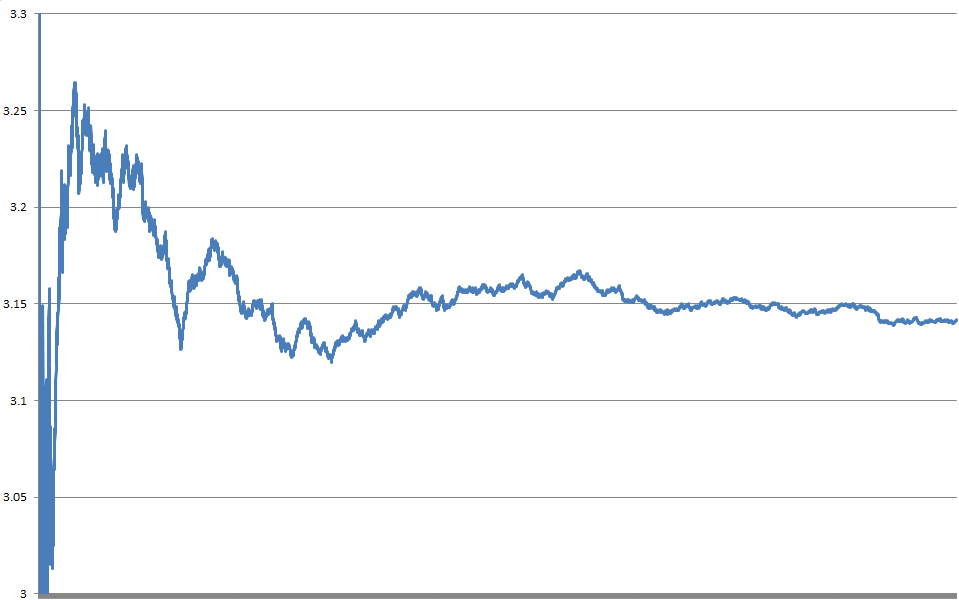
There, now wasn’t that fun? Way more than circumscribing polygons, I can tell you.